Member of the Month

KilaTsunami
October, 2024

Online

Welcome to the Newschoolers forums! You may read the forums as a guest, however you must be a registered member to post. Register to become a member today!

.999...=/=infinity

profile picture
skier58284
Posts: 1705 - Karma: 5,365
.999... is not a number. It is a limit as the variable approaches infinity [lim(n->infinity)(1-1/n)]. Infinity does not exist. Therefore, .999... does not exist. It exists in theory because we treat infinity as a number. That's fine, because it works. However, when we treat infinity as a number in theoretical applications such as limits, derivation, and integration, we have to remember that we are treating infinity as a number, and can therefore manipulate it as a number with operations such as subtraction and addition. That means we can take a hypothetical number n=1-[1/(infinity-1)], which is equal to .999.... If .999...=1, then 1-[1/(infinity-1)]=1, which means 1/(infinity-1)=0, which means 1=0(infinity-1). This is clearly incorrect, since 0x, with x being a number, is always equal to 0, and infinity is being treated as a number in this situation. Of course infinity is not a number and cannot be manipulated like this in real life, but infinity doesn't exist, so using infinity in limits also doesn't work in real life. It only works in theory when infinity is treated as a number. Claiming that .999...=1 is allowing infinity to be manipulated as a number in some ways that do not work in real life but not in others, all within the same theoretical situation. The difference between .999... and 1 is negligable to the extent that they can be treated as the same number in practical applications, but they are, by definition, not equal.
Sep 29 2013 7:07PM
143 45
profile picture
YoungJ
Posts: 447 - Karma: 883
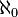Click for larger image
Sep 29 2013 7:10PM
0 0
profile picture
beansurrows
Posts: 209 - Karma: 5,526
.9999...= 1 because 1/3=.3333... and 2/3=.6666... therefore 3/3=.9999... and 3/3=1
Sep 29 2013 7:11PM
28 2
profile picture
skier58284
Posts: 1705 - Karma: 5,365
No, I took calculus 5 years ago.
Sep 29 2013 7:17PM
1 15
profile picture
-WZ-
Posts: 3600 - Karma: 6,582
math
Sep 29 2013 7:17PM
2 0
profile picture
Mr.LemonPie
Posts: 4100 - Karma: 1,625
I don't math so I don't know but surely

1/3 does not really equal .33333 repeating because .99999 does not really equal 1, that is just the only way we have of demonstrating 1/3 as a decimal.

3/3 is obviously 1, not .99999.
Sep 29 2013 7:17PM
8 2
profile picture
skier58284
Posts: 1705 - Karma: 5,365
Those are all approximations. 1/3=.333...+(1/3)*(10^-infinity)
Sep 29 2013 7:18PM
0 1
profile picture
chicken
Posts: 6843 - Karma: 2,123
i'm in physics so I get to use infinity with reckless abandon.
Sep 29 2013 7:46PM
6 0
profile picture
chicken
Posts: 6843 - Karma: 2,123
Click for larger image
Sep 29 2013 7:47PM
1 1
profile picture
chicken
Posts: 6843 - Karma: 2,123
http://www.smbc-comics.com/?id=2675
Sep 29 2013 7:47PM
2 0
profile picture
theabortionator
Posts: 51645 - Karma: 162,278
Are you trying to tell me buzz lightyear can't actually go to infinity and beyond?

I'm supposed to believe you over this guy?

Click for larger image

Lol sure bro. I think I know who's side to take on this one.
Sep 29 2013 7:57PM
16 2
profile picture
Spagett+
Posts: 3499 - Karma: 14,884
OP is ZURG
Sep 29 2013 8:14PM
13 1
profile picture
Dr.Dickless
Posts: 2620 - Karma: 1,392
this isn't correct

You're trying to look at infinity as a number, which it really isn't
Sep 29 2013 8:24PM
0 0
profile picture
skiierman
Posts: 28699 - Karma: -5,563
I wish I had a massive spitball and a giant straw right now...
Sep 29 2013 8:25PM
5 1
profile picture
ir1sh
Posts: 61 - Karma: 28
actually, they're only equal by definition... because we define them as equal
Sep 29 2013 8:38PM
1 0
profile picture
cool_name
Posts: 4295 - Karma: 3,131
op what does 999/1000 equal?
Sep 30 2013 12:23AM
0 0
profile picture
byubound
Posts: 1636 - Karma: 9,870
HA WATTA NERD
Sep 30 2013 12:32AM
1 1
profile picture
Arabian
Posts: 682 - Karma: 1,080
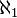No. Infinity in terms of the real number you described is not the same as the ordinal infinity defined by the term 1/n, which is in fact a countable infinity - an ordinal number denoted ω of cardinality Click for larger image. The space between any 2 real numbers is an uncountable infinity, the first uncountable ordinal ω1 with cardinality Click for larger image.

And this is not treating infinity as a number. This is treating infinity as a two point compactification of the real line with maximal suprema and infima infinity and negative infinity.
Sep 30 2013 12:33AM
3 0
profile picture
BlakeG
Posts: 1450 - Karma: 1,030
All I know is that 0.999.... Infinetly approaches 1 and OP is Zurg
Sep 30 2013 12:34AM
2 0
profile picture
Wolffy
Posts: 949 - Karma: 131
Click for larger image

Click for larger image
Sep 30 2013 12:36AM
1 3
profile picture
bigbromskier
Posts: 1175 - Karma: 330
of course it exists, because it is really just saying that whatever it is is as close as it can be to being it without actually being it.

that means that you go and go and go without actually getting to the desired goal/place/destination. in theory, that is infinity because it never ends.

so .999=infinity. it's completely theoretical, but it serves its important purpose to that end.

It's kind of like asking whether or not Vegans eat honey--it'll go and go and go through debate and argument, but, in the end, they'll be too indecisive to come to a final conclusion of yes or no. so it's always almost there, but will never get to finality.
Sep 30 2013 12:51AM
0 0
profile picture
DasGoatenshafter
Posts: 580 - Karma: 307
This is why I'm in engineering. Theoretical math is frustrating. My understanding was that a fraction can equal a geometric series which can equal a repeating decimal (repeating term of any sort) which does make the repeating decimal an exact value. I really just do mass, flow and energy balances though so there's a 60-90% chance I'm talking out my ass.
Sep 30 2013 8:35AM
0 0
profile picture
Turner.
Posts: 1987 - Karma: 11,892
meth
Sep 30 2013 9:50AM
0 0
profile picture
McLS
Posts: 1985 - Karma: 6,454
is there actually a mathematics thread on NS? Oh wait, winter isn't here yet...better come fast, a maths thread today, whats in 1 month?
Sep 30 2013 2:08PM
0 0
profile picture
Arabian
Posts: 682 - Karma: 1,080
the infinite sum of 1/n is the harmonic series - a divergent series represented by a non-repeating infinite decimal, but then, we're not looking at a power series here. We're looking an infinite sequence.
Sep 30 2013 3:38PM
0 0
profile picture
KJacks
Posts: 440 - Karma: 2,329
all i know is op like dick in his ass
Sep 30 2013 5:41PM
1 1
profile picture
ILLinoisance
Posts: 3527 - Karma: 5,398
Of all the threads i've seen in my day, this is definitely one of them.
Sep 30 2013 7:03PM
7 0
profile picture
El_Barto.
Posts: 11661 - Karma: 24,354
truer words have never been spoken.
Sep 30 2013 7:19PM
5 0
profile picture
BlakeG
Posts: 1450 - Karma: 1,030
nice.
Sep 30 2013 8:37PM
0 0
profile picture
DasGoatenshafter
Posts: 580 - Karma: 307
This is why I was happy with a C +.
Sep 30 2013 8:49PM
1 0
profile picture
HamFaceGirl
Posts: 5242 - Karma: 2,676
NERD
Sep 30 2013 9:34PM
0 0
profile picture
Ski_The_E
Posts: 1036 - Karma: 944
actually .999999... does in fact equal 1

if 0.999....=n then 9.999...=10n

therefore
10n-n=9.999...-0.999...
9n=9
n=1

0.999...=1
Sep 30 2013 9:49PM
3 0
profile picture
Peter.
Posts: 23796 - Karma: 13,014
thank god i only have to deal with physical chemistry and not math anymore


LOL who am i kidding
Sep 30 2013 10:04PM
0 0
profile picture
skier58284
Posts: 1705 - Karma: 5,365
Only yours bb ;)
Sep 30 2013 11:58PM
0 0
profile picture
skier58284
Posts: 1705 - Karma: 5,365
n=.999...
10n=9.999... - 9*(10^-infinity)
9n=9.999... - 9*(10^-infinity) - .999...
9n=9 - 9*(10^-infinity)
9n=9(1-10^-infinity)
n=1-10^-infinity
n=1-.000...1
n=.999...

ftfy
Oct 1 2013 12:03AM
0 1
profile picture
Arabian
Posts: 682 - Karma: 1,080
stop trying.
Oct 1 2013 12:36AM
2 1
profile picture
skier58284
Posts: 1705 - Karma: 5,365
Except I'm right.
Oct 1 2013 1:04AM
0 1
profile picture
Arabian
Posts: 682 - Karma: 1,080
no you're not and you're too dumb to understand why. I don't need to repeat myself 3 times.
Oct 1 2013 1:37AM
1 1
profile picture
TannerBalls
Posts: 3197 - Karma: 1,310
yep
Oct 1 2013 1:41AM
1 0
profile picture
Ski_The_E
Posts: 1036 - Karma: 944
Click for larger image
Oct 1 2013 2:17PM
2 0
profile picture
Top_Gun
Posts: 258 - Karma: 469
This thread is way too complicated for me

Click for larger image

Oct 2 2013 1:44PM
0 0
profile picture
ForrestW
Posts: 451 - Karma: 56
lol... wooooshh
Oct 2 2013 1:57PM
0 0
All times are Eastern (-5)